##Infinite Noise Multiplier

The Infinite Noise Multiplier (INM) is an architecture for true random number generators (TRNG). Besides being simple, low-cost, and fast, it is easy to get right, unlike other TRNGs.

INMs are suitable for both board level implementation, and ASIC implementation. Speed is limited by the speed of a voltage buffer and comparator, and can run in excess of 100 Mbit/second per second with high performance components. Cheap solutions with CMOS quad op-amps can run at 6Mbit/second.

Adjacent bits from an INM are correlated, so whitening is required before use in cryptography. INM output has a highly predictable amount of entropy for easy estimation of bits added to an entropy pool.

The Problem: Noise Sensitivity, and Signal Injection

True random number generators are very difficult to get right. Generally, they amplify a tiny noise signal, perhaps only a microvolt in amplitude, by a factor of millions or billions, until the signal is an unpredictable digital signal. This signal is then sampled to see if it's a 0 or 1.

The problem with this aproach is the weak noise source can easily be overridden by other nearby signals, which may be under the control of an attacker. Power supply noise can cause zener diodes to avalanche with predictable timing. Thermal noise can be overridden by nearby radio sources, such as EMI from a CPU. Oscillator drift can be controlled through syncrhonous power-supply noise. Jitter can be controlled through cross-talk and power rail droop. On ICs, substrate currents can override thermal noise. Cross talk strong enough to override these tiny sources of noise can be introduced through radio waves, inductive coupling, capacitive coupling, or even "microphonics", due to physical vibrations in the system. These circuits are sometimes even light sensitive.

Systems built with massive amplification of tiny noise sources often require power supply filters, EMI shielding, and even light shielding, and even then remain difficult to prove secure. Such systems can be difficult to audit, because their signal traces are inaccessible behind layers of shields.

Intel's RDRAND instruction is a perfect example. It uses massive amplification of thermal noise to determine the power-up state of a latch. Unfortunately, this source of entropy is highly power-supply, cross-talk, and substrate current sensitive. Intel claims to have carefully shielded their thermal noise source, but without a thorough pubic audit of both the design and layout, including all potential sources of interference, it is not possible to trust the RDRAND instruction as the source of entropy for cryptography.

With such strong sensitivity, these TRNG architectures are potential targets for signal injection by an attacker, who can cause the TRNG to generate his desired output rather than true random data.

The Solution: Modular Multiplication

Unpredictable noise sources are tiny, and must be massively amplified to be used by an TRNG. Other TRNG architectures amplify these signals until they saturate, becoming digital 1's and 0's. They rely on careful design and shielding to keep outside signals from influencing the noise source.

For example, if we amplify a tiny noise source by 1 billion in a system that saturates at 3.3V, then 1uV of noise will be amplified causing the output to be about 3.3V. An attacker need only introduce at least -1uV to cause the TRNG to saturate at 0V instead. An attacker even this tiny influence over the noise source can entirely control the output.

This is the wrong aproach. Instead, TRNGs should use modular multiplication to amplify their noise source, because modular multiplication never saturates.

If we multiply a 1uV peak by 1 billion modulo 3.3V, then the result will be about 0.3V, which will result in a ditital 0. If an attacker subtracts 1uV, causing our noise source to be at 0.0V, then after amplification, the output is 0V, which still results in a 0. In fact, without knowing the current amplituded of the noise source, there is no signal an attacker can add to our noise source that will result in a desired output. He may be able to flip the output bit, but since it was already random, his signal injection fails to control the result, which is still random. In fact, an attacker's injected signal causes the output to be more random, since an attacker is a nice unpredictable source of entropy! Infinite Noise Multipliers add entropy from all noise sources, even those from an attacker.

Variations

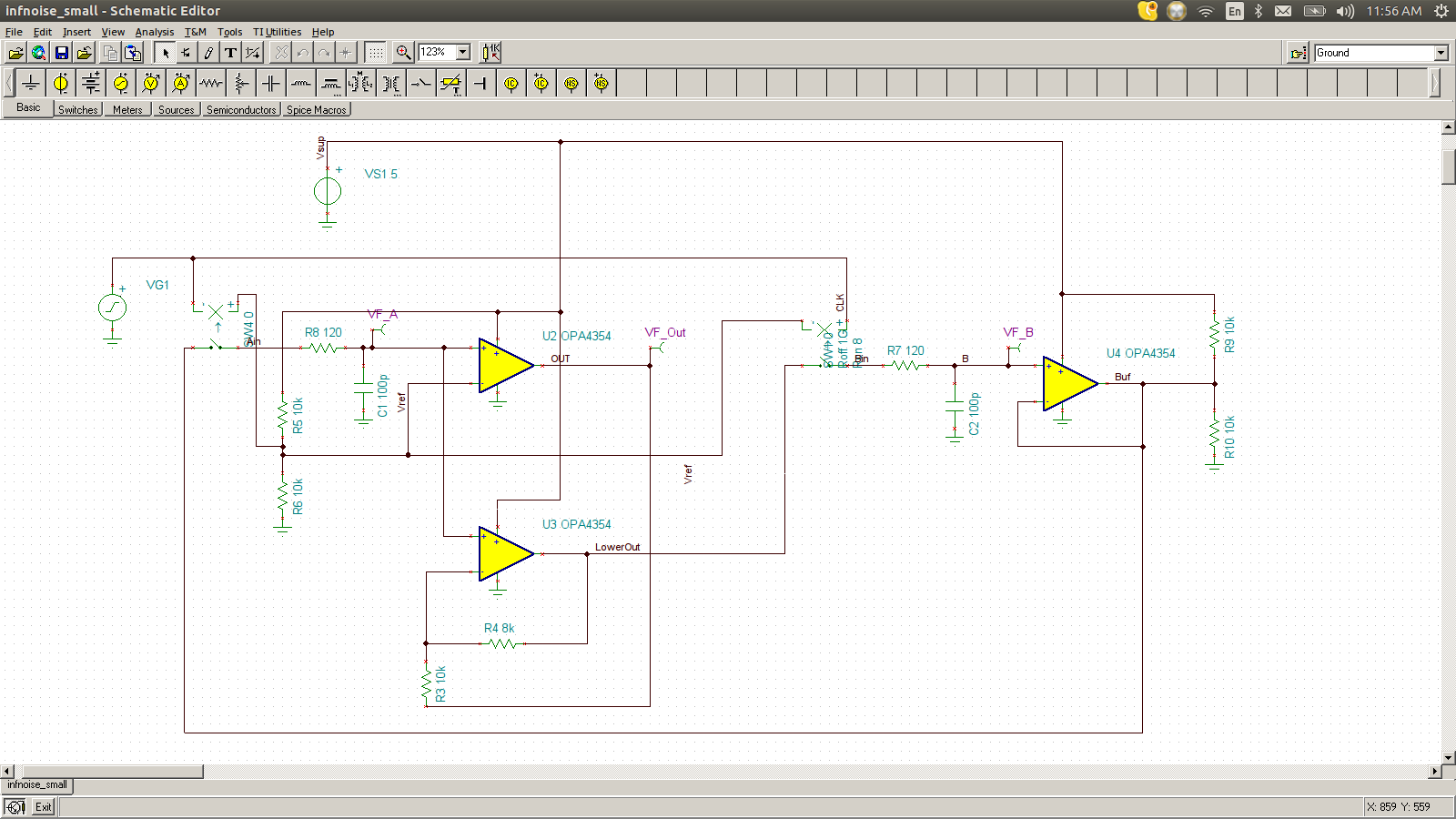
There are currently 3 versions of Infinite Noise Multipliers documented here. The infnoise_small directory describes a low part-count design that works well with op-amps which have rail-to-rail inputs and outputs. It runs at 4MHz, outputing 0.84 bits worth of entropy on each clock (loop gain = 1.8), for a total of 3.36Mbit of entropy produced per second. The infnoise_fast directory contains a 50% faster design that uses a few more resistors and an additional op-amp. This design is suitable for use with a wide range of op-amps. It runs at 6MHz, outputing 0.84 bits worth of entropy on each clock (loop gain = 1.8), for a total of 5.04Mbit of entropy per second.

Because Infinite Noise Mulitpliers are switched-capacitor circuits, it is important to use components with low leakage, like the OPA4354 CMOS quad op-amp from TI. Op-amps with below 1nA of input bias current will enable running at lower frequencies with less power.

To reproduce these simulations, download the TINA spice simulator from Ti.com.

There is also a CMOS version described here.

Simulations

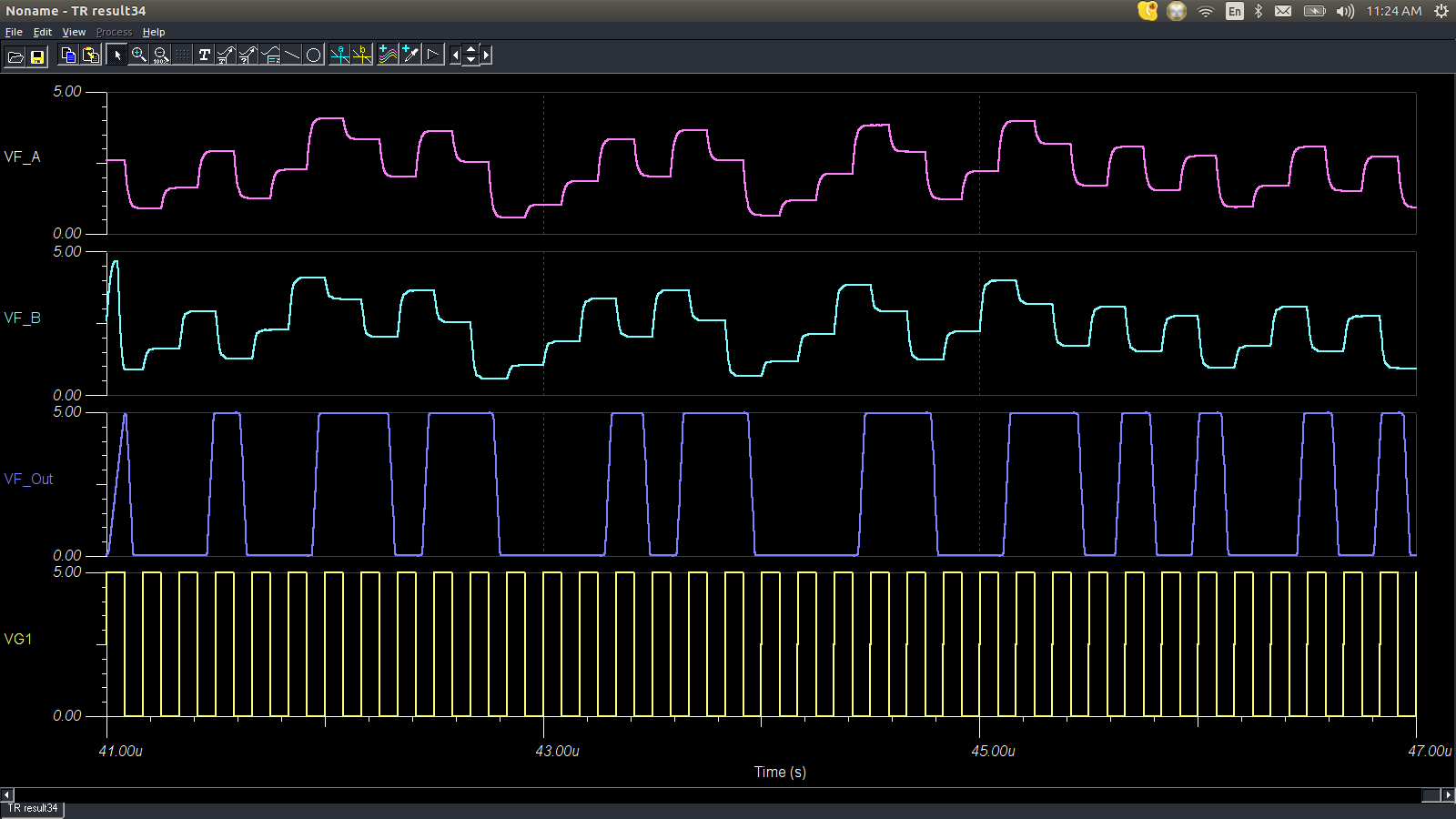
LTspice was used to simulate the small and fast variations. Here are simulation waveforms for the small verision:

And again for the fast version.

Design Analysis

The ideal case is easy to understand. Each clock cycle the value A is multiplied by 2X. If the result is above Vref (typically 1/2 supply), then the comparitor will output a 1, and if it is below Vref, it will output a 0. Both should occur with equal probability, with no correlation between bits. This has been verified to some extent with a C simulation and dieharder.

In the ideal case, the circuit simply multiplies a signal by 2X every cycle. If you imagine the value as being between 0 and 1, and represented in binary, when you multiply by 2, you simply left-shift the value. The value out is the bit that shifts from the 1/2 position to the 1's position. If a 1 was shifted out, we remove it, so that it is again between 0 and 1.

However, due to accuracy limitations on real components, we cannot multiply by exactly 2X every cycle. When the loop amplification is < 2X, the entropy per output bit is reduced, but can be easily computed. If E is the entropy per bit, and A is the loop amplification, then:

E = log(A)/log(2)

This provides a simple way to calculate the entropy added to an entropy pool per bit.

The simplest way to understand why this is true is to imagine representing a value in base A, rather than base 2. For example, if a random 3-bit binary value from 0 to 1 is converted to base sqrt(2), then it will take up to 6 bits. The value 0.625 = 0.101 in binary. In base sqrt(2), it is 0.010001, because 0.01 base sqrt(2) is 1/2, and 0.000001 base sqrt(2) is 1/[sqrt(2)^6] = 0.125.

Entropy, as used here, describes the possible number of equal probability outcomes. If there are 12345 equally likely outputs from an INM, then that is considered to be log2(12345) = 13.59 bits of entropy. In the idean case where A is exactly 2, we can easily see that an unbiased true random bit is shifted out each cycle. Since converting an N bit sequence base 2 to an M bit sequence base A requires log(A)/log(2) bits, those same 2^N equally likely states are encoded by M bits base A. An entropy pool benefits the same from N true random bits as M biased bits in this case.

The program infnoise.c directly measures the entropy of INM output, and compares this to the estimated value. Simulations show that they correlate well.

There are two significant variations on the INM architecture so far. The first one, done with CMOS transistors, which is suitable for an IC implementation, does a multiply by 2 by stacking capacitors, and if the result is greather than Vref, it subtracts a value (using a capacitor again) to reduce the value to below Vref. This is a literal implementation of multiplication mod Vref.

The board level versions were simplified using a couple of tricks. First, multiplication by 2 modulo Vsup is accomplished by multiplying relative to either GND or Vsup. When multiplying relative to GND, a 0.2V signal becomes 0.4V. When multiplying relative to a 3V Vsup, a 2.8V signal becomes 2.6V. The math comes out the same as if I'd multiplied relative to GND, and simply subtracted Vsup if the result was > Vsup:

Vsup - 2*(Vsup - A) = Vsup = 2*Vsup + 2*A = 2*A - Vsup

So, we multiply by 2 either way, and only subtract out Vsup if needed. This is identical to multiplication modulo Vsup.

A second trick used to create the "small" version was to notice that the output of the comparator could be used to combine both multiplier op-amps into 1. This abuse of the comparator output needs to be carefully checked. In particular, the output is generally treated as a digital signal, but in this case, it is used as an analog singal. Care should be taken not to load the OUT signal significantly, and also to be sure the comparator can drive the resistive load with no more droop than the buffer driving signal B. However, don't be concerned about noise. Cross-talk is OK. It can only add to the entropy.

Free As in Freedom

I, Bill Cox, came up with the original CMOS based Infinite Noise Multiplier architecture in 2013, and the board level versions in 2014. I hereby renounce any claim to copyright and patent rigts related to this architecture. I'm giving it away emphatically freely. Furthermore, I am aware of no infringing patents and believe there are none. It should be entirely safe for use in any application.